Computing Coupled Similarity

Ich habe dieser Tage meine Masterarbeit mit dem schönen Titel „Computing Coupled Similarity“ eingereicht. Coupled Similarity ist ein bestimmter Begriff davon, was für Zustände von Programmen gleich sind. Natürlich funktioniert der Begriff nicht nur für Programme, sondern auch für allgemeinere Abläufe. Es gibt sehr viele Gleichheitsbegriffe für solche Systeme. Dazu gehören jeweils Algorithmen, um die Gleichheiten zu ermitteln. Für Coupled Similarity wurde wohl bisher vergessen, so einen Algorithmus zu entwickeln, und das ist es, was ich in meiner Masterarbeit nachhole.

Leute mit Mathe/Informatik-Hintergrund können direkt in „Computing Coupled Similarity“ reinschnuppern. Für alle anderen folgt eine alltagsverständlichere Erklärung.

„Gleich“ bedeutet für Systeme in unserem Sinne, dass man sie mit einem bestimmten Sortiment an Beobachtungen „von außen“ nicht unterscheiden kann. Wenn man tiefer reinschauen könnte, würden einem vielleicht Unterschiede auffallen. Ein Gleichheitsbegriff wie Coupled Similarity funktioniert jetzt so, dass man zwei Innensichten von Systemen hat (z.B. zwei Programmquelltexte) und der Begriff definiert, ob diese zwei Systeme von außen gleich sind. Gleiche Systeme verhalten sich dann für Kontexte, in denen sie stehen könnten, jeweils gleich.

Gefangene Philosoph*innen

Stellt euch zum Beispiel vor, dass wir als Beobachter*in vor einer Gefängnismauer stehen, die nur ein kleines Fenster hat. Wir haben eine kleine Trillerpfeife, mit der wir pfeifen können (p).Auf der anderen Seite sind drei Philosoph*innen A, B und C eingesperrt, die auf einen kleinen Tritt steigen (s) können und durchs Fenster gucken (f).A passt nur alleine auf den Tritt. B und C sind dünner und können gemeinsam darauf steigen. Durchs Fenster gucken kann aber nur eine*r von ihnen. Wenn wir die Pfeife blasen, dann versuchen die Philosoph*innen auf den Tritt zu steigen und aus dem Fenster zu gucken und uns zu winken. Die Situation kann von innen gesehen folgende Zustandsverläufe nehmen, wobei Kreise Zustände und Pfeile Zustandübergänge („Transitionen“) ausdrücken:Von außen wissen wir, wann wir die Pfeife pusten und wann uns A, B oder C aus dem Fenster zuwinkt. Die Vorgänge, auf den Tritt zu steigen und sich zum Fenster zu strecken (s und f), stehen in Klammern, weil sie intern sind. Auf den Zustandsverläufen, bei denen am Ende B oder C uns winken, gibt es nur ein (s), weil sie gemeinsam auf den Tritt klettern.

Stellen wir uns jetzt vor, es sähe drinnen minimal anders aus: Der Tritt ist schmaler, sodass direkt nur eine*r der Philosoph*innen darauf passt.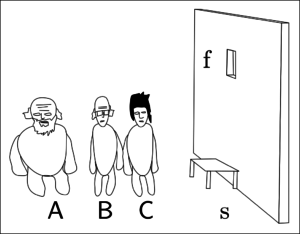Dann würde sich in den Zustandsverläufen schon bei (s) entscheiden, wer uns am Ende winkt:Und jetzt ist die Preisfrage: Sind diese beiden Systeme von außen gleich, das heißt: nicht unterscheidbar? Und wie lässt sich das formalisieren?

Simulation und Similarity

Einer der grundlegendsten Begriffe für Gleichheit zwischen Systemzuständen ist Simulation. Ein Zustand wird von einem anderen simuliert, wenn dieser mindestens gleich viel machen kann. Das ist keine ganz intuitive Wortwahl, aber so ist sie nun einmal. Simulationen sind auf eine bestimmte Art abgeschlossene Relationen zwischen Zuständen. Das heißt, wenn sie bestimmte Zustände in Beziehung setzen, dann müssen sie auch bestimmte andere in Beziehung setzen. Schematisch sieht Simulation so aus:Gelesen: Wenn Zustand a durch Zustand b simuliert wird (blauer Pünktchenpfeil), dann muss für jeden x-Übergang (schwarzer Pfeil), den a machen kann, auch b einen x-Übergang machen können, sodass der Zielzustand von a weiterhin durch den Zielzustand von b simuliert wird. Im Bild also: Wenn es die Pfeile oberhalb der Strichellinie gibt, muss es auch die unterhalb geben.

Die beiden vorgestellten Systeme simulieren sich gegenseitig im Sinne von schwacher Simulation (Weak Simulation). Schwach bedeutet dabei, dass interne Zustandsübergänge übersprungen werden können. In unserem System bedeutet das, dass die p-Transition zum Beispiel direkt in den Zustand springen kann, in dem A aus dem Fenster winkt. Von außen ist nicht sichtbare, wie viel interne Aktivität zwischen den Zuständen liegt. Das Schema sieht also genau genommen so aus: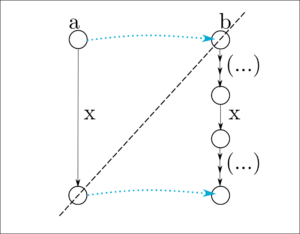Auf der rechten Seite dürfen beliebig viele interne Transitionen vor und nach der x-Transition eingefügt werden.

Wenn man solch eine Simulations-Abbildung angeben kann, dann herrscht „Weak Similarity“. Schauen wir uns eine Weak Simulation auf dem Philosoph*innen-System an.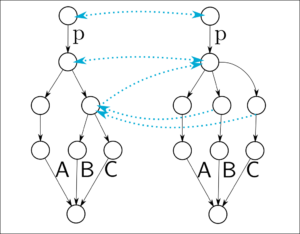Für den unteren Teil des Zustandsbereichs ist die Simulationsbeziehung klar, der ist ja identisch. Darum habe ich nur für den oberen Teil eingezeichnet, welcher Zustand durch welchen anderen simuliert wird (blaue Pfeile). Spannend ist der Bereich, in dem die Entscheidung stattfindet. Hier ist die Simulationsbeziehung nicht ganz symmetrisch. Auf der rechten Seite werden zwei Zustände durch denselben Zustand auf der linken Seite simuliert. Der links kann noch A und B, während die rechts bloß noch eins von beidem können – aber gerade das reicht ja zum simuliert werden. Genau so kann der linke Zustand weniger als der Entscheidungsknoten auf der rechten Seite und wird entsprechend simuliert.

Weak Similarity stellt also fest, dass die beiden Systeme mit schmalem und breitem Tritt von außen ununterscheidbar sind.

Simulation ignoriert Trolle

Gegenseitige Simulation ist allerdings ein sehr unpräziser Gleichheitsbegriff. Schauen wir uns folgendes System an, in dem außer den Philosoph*innen auch noch ein Troll in der Zelle sitzt, der sich auf den Tritt hocken kann.Der Troll kann auch (s) ausführen und dann dort stehen bleiben, sodass kein*e Philosoph*in mehr zum Fenster kommt. Das führt eine Sackgasse im Zustandsraum ein. Sobald der Troll auf dem Tritt sitzt, geht’s nicht mehr weiter. Draußen würden wir nur sehen, dass wir nichts sehen.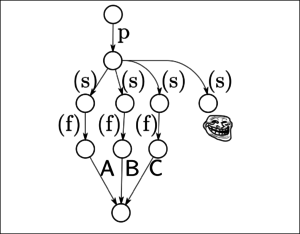Schwache Simulation hält den Unterschied nicht für relevant, wie folgender Ausschnitt aus einer Simulation zum Trollsystem zeigt.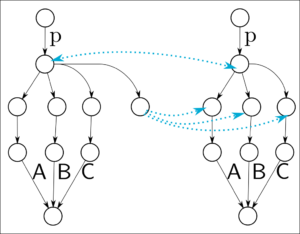Der Trollzustand wird durch alle möglichen Zustände simuliert, da er ja weniger machen kann als sie alle (nichts). Dadurch können Zustandsübergänge zum Trollzustand kinderleicht simuliert werden. Für alle anderen Zustandsübergänge ist die Simulation auch klar.

Schwache Simulation ist nicht symmetrisch genug. Es ist ihr egal, dass der Trollzustand keinen der direkten Nachfolgezustände der Entscheidung auf der rechten Seite simuliert.

Wer das System mit und ohne Troll unterschieden sehen will, braucht einen penibleren Gleichheitsbegriff als Weak Similarity. Genau das eröffnen Coupled Simulation und Coupled Similarity.

Coupled Simulation und Similarity

Coupled Simulation führt eine schwache Art von Symmetrie-Anforderung, Coupling, ein. Das fordert, dass es ab und zu auch Rückpfeile zu geben hat: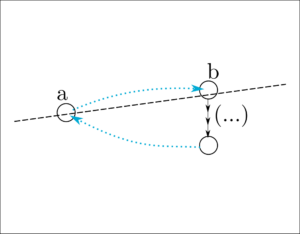In Worten: Sobald a durch b simuliert wird, muss b sich ohne sichtbare Aktionen in einen Zustand entwickeln können, der a wieder simuliert.

Diese Anforderung verbaut, dass der Trollzustand durch die unmittelbaren Nachfolgezustände der Entscheidung auf der rechten Seite gekoppelt simuliert werden kann. Zwischen dem Troll-System und den beiden anderen Systemen herrscht keine Coupled Similarity!

Für unsere zwei Ausgangssysteme gibt es hingegen eine gekoppelte Simulation.Nach jedem blauen Pfeil, der nur in eine Richtung weist, kommt noch im durch interne Transitionen erreichbaren Bereich ein Pfeil, der in die Gegenrichtung weist. Es entstehen Dreiecke aus einem blauen Simulationspfeil in die eine Richtung, schwarzen Schritten und blauen Pfeilen zurück zum Ausgangszustand. Das ist genau das, was Coupling fordert.

Coupled Similarity ist eine Verallgmeinerung der weitaus bekannteren „Weak Bisimilarity“. Vereinfacht gesagt, fordert letztere direkt Symmetrie, also dass alle blauen Pfeile in beide Richtungen weisen. Das ist ein Spezialfall von Coupling. Statt beliebig vielen internen Schritten, dürfen bei Symmetrie nur immer genau null interne Schritte gemacht werden bis zum blauen Rückpfeil.

Weak Bisimilarity lehnt jedoch die Gleichheit unserer Ursprungssysteme ab. Sie behauptet also, dass man von außen den Unterschied beobachten könnte, ob ein oder zwei Philosoph*innen auf den Tritt steigen, bevor einer aus dem Fenster schaut. Der Grund dafür ist, dass der halb-entschiedene Zustand im Zustandsgraph nicht symmetrisch simuliert werden kann.

Trotzdem sind Weak Bisimilarity und Coupled Similarity sich noch recht ähnlich. Beispielsweise: Falls es keine internen Transitionen gibt, decken sie sich. Weak Similarity hingegen bleibt auch in solch einer Situation gröber als die anderen beiden.

Ich denke, die drei Beispielsysteme illustrieren recht gut, warum Coupled Similarity ein ganz vernünftiger Begriff davon ist, wann zwei Systeme mit internen Zustandsübergängen sich von außen gesehen gleich verhalten. Allerdings ist Coupled Similarity auch in der Informatik eher eine arkane Nummer.

Computing Coupled Similarity

Inhalt meiner Masterarbeit war jetzt, diese blauen Pfeile zwischen Zustandsräumen für Coupled Simulation zu finden.

Gemeinerweise ist ihre Berechnung, wie ich zeigen konnte, etwas komplexer, als blaue Pfeile zum Beispiel für Weak Bisimulation zu suchen. Egal, wie sehr man an seinen Algorithmen schraubt, man wird immer etwas mehr zu betrachten haben als für Weak Bisimilarity.

Im Einzelnen habe ich eine spieltheoretische Charakterisierung für Coupled Simulation angegeben, aus der sich ein Algorithmus ergibt. Die Korrektheit davon habe ich mit dem Beweiswerkzeug Isabelle/HOL maschinenverifizierbar nachgewiesen.

Spaßeshalber habe ich den Algorithmus auch noch mit Apache/Flink implementiert. Das ist diese Art von Software, mit der man auf großen Datenmengen parallelisiert Berechnungen anstellen kann. Sonst begehen Leute mit sowas ihre Big-Data-Datenschutz-Verbrechen.

Leider stellte sich heraus, dass Coupled Simulation zu ermitteln mit meinem armen kleinen Rechner leider schon bei wenigen zehntausend Zuständen zu heftig ist. Damit kann ich aber leben, weil offenbar auch niemand anders Simulationsbeziehungen, die gröber sind als Weak Bisimilarity, für wirklich große Zustandräume berechnet bekommt. Also: Im Ergebnis gut genug, um es einfach mal als Masterarbeit abzugeben.

Für weitere Details schaut ihr wohl am Besten in ebendiese und spielt mit dem begleitenden Webtool CoupledSim Fiddle.